The Sun Diver: Combining solar sails with the Oberth effect

C.A.L. Bailer-Jones

A highly reflective sail provides a way to propel a spacecraft out of the solar system using solar radiation pressure. The closer the spacecraft is to the Sun when it starts its outward journey, the larger the radiation pressure and so the larger the final velocity. For a spacecraft starting on the Earth's orbit, closer proximity can be achieved via a retrograde impulse from a rocket engine. The sail is then deployed at the closest approach to the Sun. Employing the so-called Oberth effect, a second, prograde, impulse at closest approach will raise the final velocity further. Here I investigate how a fixed total impulse (Δv) can best be distributed in this procedure to maximize the sail's velocity at infinity. Once Δv exceeds a threshold that depends on the lightness number of the sail (a measure of its sun-induced acceleration), the best strategy is to use all of the Δv in the retrograde impulse to dive as close as possible to the Sun. Below the threshold the best strategy is to use all of the Δv in the prograde impulse and thus not to dive at all. Although larger velocities can be achieved with multi-stage impulsive transfers, this study shows some interesting and perhaps counter-intuitive consequences of combining impulses with solar sails.

American Journal of Physics, 89, 235 (2021) (featured article)
[PDF] [arXiv] [journal (open access)] [poster]

What if we had a very large Δv available?

In the paper I only explore the cases in which the total Δv is less than the spacecraft's initial (circular) orbital velocity, v_i. This is because if Δv = v_i then the spacecraft would - in theory, with the Sun as a point mass - drop into the Sun and so achieve infinite velocity. But what about in practice? I note this at the end of section III: if we had Δv ≥ v_i then use as much as fuel as necessary to drop as close as practically possible to the Sun, then at perihelion open the sails and use the rest of the fuel in a prograde boost. This would achieve the maximum velocity upon return to the initial orbit (and therefore also at infinity, provided the sail and/or boost are enough to reach infinity at all).

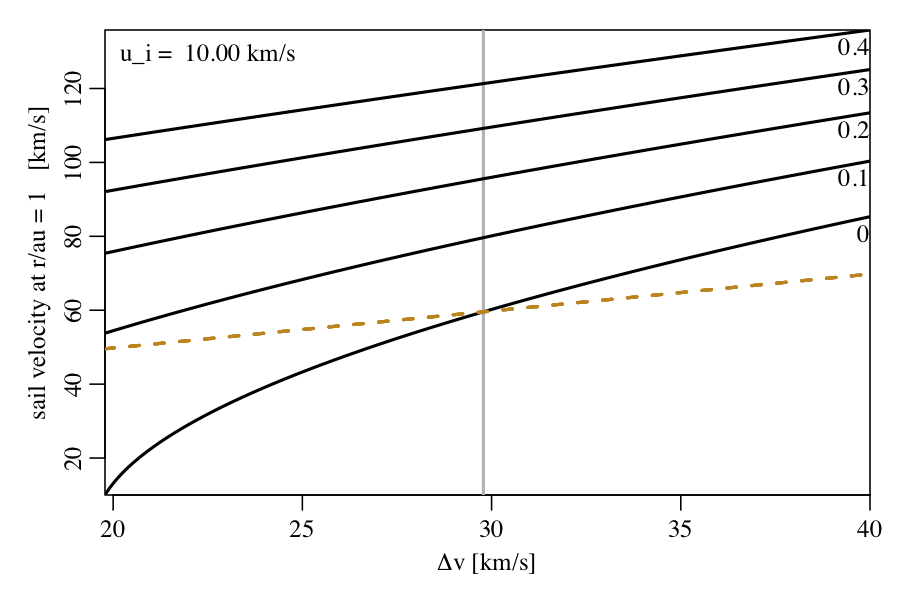
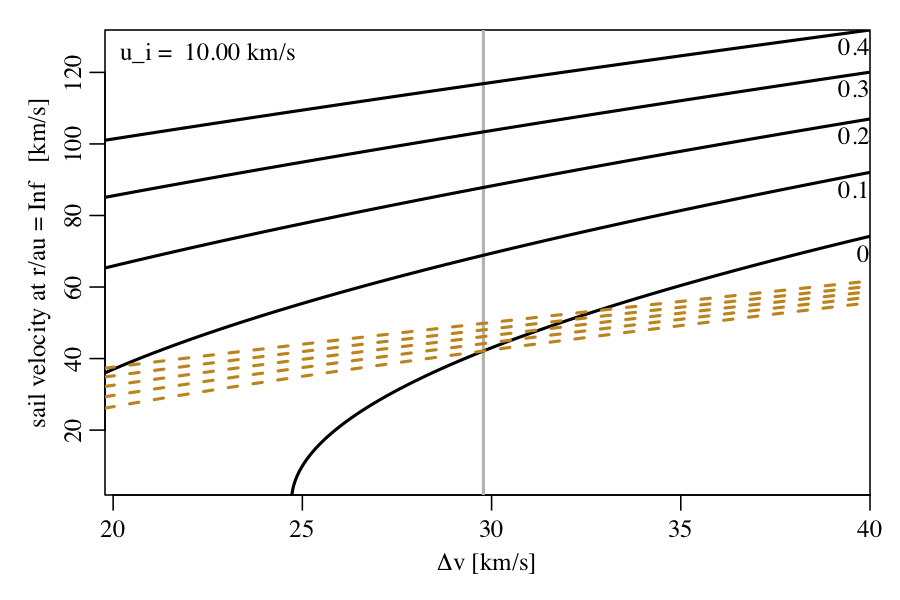
This is illustrated in the top left figure below. Starting in an initial circular orbit of radius 1 au, the spacecraft initially uses some of its fuel to perform a retrograde boost of v_i - u_i to decelerate it from v_i = 29.8 km/s to u_i = 10.0 km/s. This causes the spacecraft to dive to a perihelion distance of 0.060 au where its velocity will be 167 km/s. The rest of the fuel is used here to provide a prograde boost – of Δv - (v_i - u_i) – which together with the now open sail propels the spacecraft outwards. The plot shows how the velocity upon return to 1 au varies with Δv for various lightness numbers (shown at the top right). The orange dashed line shows the no dive case, i.e. all Δv is used in a prograde boost in the intial orbit (this is of course the same for all lightness numbers). For no sail (lightness=0), we see that if Δv < v_i then the dive always results in a lower return velocity than not diving (the vertical grey line shows Δv = v_i). But if we had a larger Δv, then it is worth diving. Note that for smaller Δv the no-sail spacecraft cannot even get to infinity, as shown in the bottom plot.

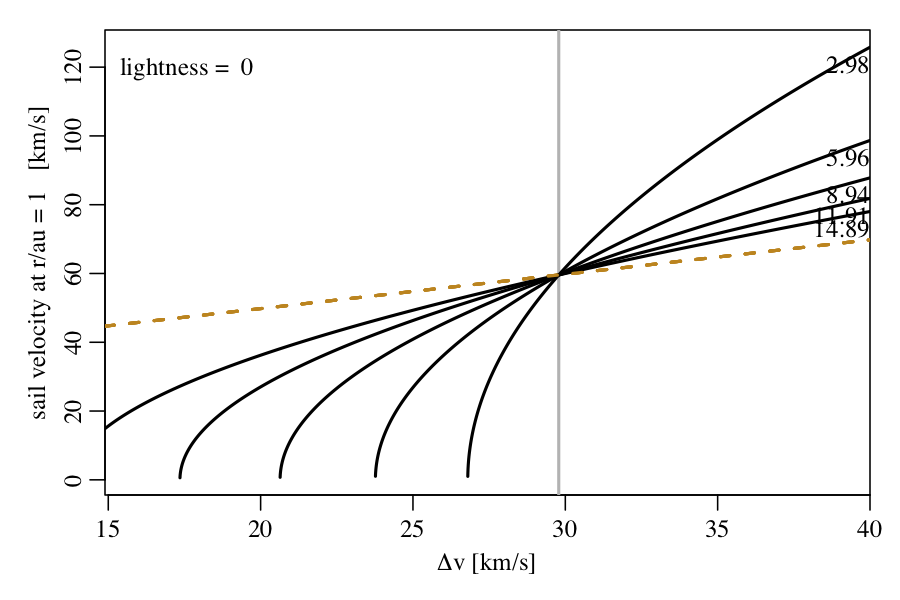
Another way of looking at this is in the plot on the top right. This plot has the same axes as the one on the top left, but is now for fixed lightness=0 and variable u_i (indicated in km/s at the top right). As long as Δv < v_i the dive is not worth it, but above it us. This issue of diving for the non-sail case has also been investigated by Blanco & Mungan (2021). Their Figure 2 likewise shows that the dive (they call it "Oberth") gives a larger velocity (at infinity in their plot) only once Δv > v_i (Δv/v_o > 1 in their notation). Their paper also investigates, again for the no-sail case, the three-impulse bi-elliptic manouevre I mention in section IV.C (they call it "Edelbaum manoeuvre"). This is more fuel-efficient than the two-impulse manoeuvre, and is superior to the no-dive case ("direct escape") already for Δv slightly below v_i.

Of course, for a spacecraft (with or without sail) in a 1 au orbit about the Sun, a Δv of order 30 km/s is practically unachievable for a chemical rocket (see endnote 11 in my paper). But for a spacecraft in a much higher orbit, or for one orbiting around a lower mass body - recall that v_i = √(GM/ r_i) - diving even without a sail may become an option.

Return to my homepage.