 |
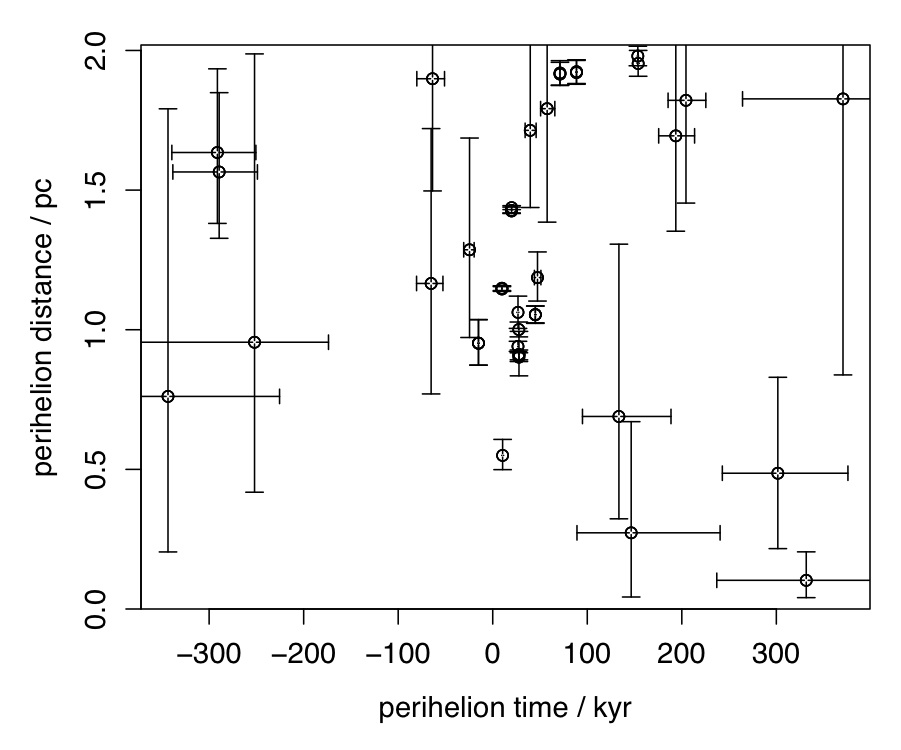
| The closest encounters with the Sun in space and time. The open circles show the expected perihelion distance vs. the expected perihelion time for each star. The error bars mark the 5% and 95% quantiles of the distributions for each star, which together form a 90% confidence interval on the estimate. |
The goal of this study was to find out whether any stars have come, or
will come, close enough to the solar system to potentially have a
measurable effect on the Earth. One possible consequence of such an
encounter is a perturbation of the Oort cloud, such that comets could
eventually be sent into the inner solar system. These in turn could
hit the Earth, which could have significant consequences for life on
Earth. This study is limited to stars for which we have sufficient
data (accurate distances and velocities), which in turn limits us to
stars currently within a few 10s of pc from the Sun (up to a few
100pc, but not at all complete over that volume). I find that about 40
stars have come or will come within 2pc within ± 20 Myr from now. Some
of these stars have poor data, however. Several of these encounters
were known before, but the significance of my study is that I (1) have
used more recent data or reanalyses of data to produce hopefully more
accurate results, and (2) compensate more rigorously for the
uncertainties in the data, so that I can attach probabilities to my
statements. That is, I can say that a star has so-and-so probability
of approaching within some specified distance at some time.
What made you decide to investigate this problem?
This study is part of a larger programme of mine named "astroimpacts" (see this link) to study the potential impact of astronomical phenomena on the Earth. That astronomical phenomena effect the Earth is obvious when you think of the day/night cycle and seasonal variations which pace human life. But there are phenomena on longer time scales of relevance too, such as the 11-year solar cycle, or variations in the Earth's tilt and orbit on 10s to 100s of kyr scales, which have played a major role in long-term climate change (such as ice ages). Zooming out even further in time, there is evidence for nearby supernovae having had an effect on the Earth within the past few Myr, and it is very likely that an asteroid made a contribution to the mass extinction at the end of the Cretaceous period 65 Myr ago. I am interested in the history of the Earth, and astronomical phenomena have clearly played a role in this. But what role precisely, how significant, and what can we expect to happen in the future?
This general problem has been investigated by others, but some studies have used questionable methods or cherry-picked data to reach weak conclusions. Their conclusions don't always stand up to statistical scrutiny. I summarized some of the issues in a review paper in 2009.
This particular study is one aspect of this larger project, and indeed
one which I hope Gaia can improve upon (see this
question). As I am working in the Gaia consortium, these seemed a
natural combination of my interests.
How did you you do your calculations?
The current positions and velocities of the stars are given by the
observational data. I then trace their orbits backwards and forwards
in time using Newton's laws. (These orbits are not straight lines
because of the gravitational force of all the stars and dark matter in
the Galaxy, as represented by a simple smooth model of the mass
distribution in the Galaxy.) This tracing cannot be done analytically
(by solving a simple equation), so I use a standard numerical
technique. (This basically involves reconstructing the orbit in a lot
of very short straight line segments.) I also do the same for the Sun
(as it too is moving through the Galaxy). I then identify when the
star and Sun were closest to each other and measure their
separation. I then repeat the procedure, but changing the initial
coordinates (position and velocity) of the star at random according to
its observational errors. I do this 10,000 times for each star, which
allows me to build up a probability distribution over how close the
star came to the Sun (and likewise a probability distribution over
when the closest approach occurred and what its speed was.) In other
words, I translate the uncertainties in the observed data into
uncertainties in the closest approach of the star.
Why do you report "confidence intervals"?
As mentioned above, the data on the stars' positions and velocities have noise (uncertainties), so we cannot be 100% sure at which distance a star will pass from the Sun. In my work I estimate the probability distribution over the closest approach distance for each star. This probability distribution is the main result. But of course we would like to summarize it in some way, e.g. what is the expected distance, or what is range of likely distances. None of these probability distributions can be reliably summarized with a single number: many of them are broad, and some of them are skew. For this reason I report the 90% confidence interval: the star has a 90% chance of having a true perihelion lying in this interval. (For those mathematically minded, I show in the appendix of the paper that this is indeed a Bayesian rather than a frequentist confidence interval.) I also report a mean for convenience, but I could equally well have reported the median or mode. Each has its advantages and disadvantages as a single summary. The mean will generally be slightly larger than the median for these distributions, as they have a positive skew, but the differences are mostly very small. I also report the probability that each star approaches within 0.5pc, 1pc, and 2pc.
Note that I do not report a standard deviation. Often in science one
sees results like "x = m ± e", such as "x = 6 ± 2", where
"m" is the measurement and "e" the standard deviation, used as a
measure of the uncertainty in m (the spread of the
distribution). Usually this means that we believe x has a Gaussian
distribution and the 68% confidence interval is from m-e (=4) to m+e
(=8). But what if the measurement, m, was smaller? Can we report
something like "x = 1 ± 2"? If the quantity x can be negative,
then yes. (Note that in the previous example there is also a finite
probability that x can be negative.) But if x is strictly positive,
like the distance to something, then this makes no sense. In that case
reporting uncertainties in terms of standard deviations also makes no
sense. (The Gaussian distribution is then also not appropriate, because it
extends from minus infinity to plus infinity.) That's why I report
confidence intervals, not "m ± e".
Do your results change much if you use the median rather than the mean?
No. The changes are very small. See this summary.
The closest encounter is Hip 85605. How reliable is this?
As I note clearly in the paper: not very! Part of the problem is that there is a second star just 22 arcseconds away, Hip 85607. Due to the size of the field-of-view of the Hipparcos detector (photomultipliers with a modulating grid), stars with separations around this size were particularly problematic in the Hipparcos data reduction. This is documented in the literature (e.g. volume 1 of the Hipparcos catalogue), and is a bit technical, so I won't explain it here. As I discuss in my paper (section 4.2), there is considerable uncertainty about the astrometry of this particular star, both in the original Hipparcos catalogue and in van Leeuwen's re-reduction. van Leeuwen looked at this system again on my request, and while the data I use are a reasonable solution, they remain problematic (as he himself emphasised). In particular, the distance corresponding to the parallax combined with the apparent magnitude are inconsistent with its colour, if it is a main sequence star.
This is one of several objects in my list which have low confidence data (several others are due to unlikely radial velocities), as discussed in section 5.4 of the paper. While some commentators note the problem with this star, not all mention that I pointed it out already. Indeed, the problem of Hip 85605 was known long before my paper - see the papers I cite. Rather than removing problematic cases in an ad hoc fashion from my results, I decided to include all, and then to comment on the nearest ones (in section 4.2).
While I suspect we just have problematic astrometry in the case of Hip
85605, it would be useful to get a spectrum of this star to learn
more. But to get a reliable distance independent
of assumptions about the star itself, we need to get new astrometry
(as Gaia will).
I have read that GL 710 is the star to come closest to the Earth? Do you confirm this?
It's important to remember that my study is limited to stars which have both astrometric measurements from Hipparcos and measured radial velocities. For this study I used around 50,000 stars, far fewer than the actual number of stars in the Galaxy (which is around 100 to 1000 billion). We simply don't yet have the data on many more stars (but this will change soon: see the question on Gaia). Earlier studies were also limited to Hipparcos (or, in the pre-Hipparcos era, very small sets of stars). So we probably haven't found the closest approaching star yet.
The closest encounter (in terms of the expected distance) I find is Hip 85605, which has a 90% probability of coming between 0.04 and 0.20 pc between 240 and 470 kyr from now. However, this star has questionable data, and while this is the best we can say based on those data, I would not say this is a strong conclusion. My second closest star in is GL 710. I find a 90% probability that its perihelion (closest approach to the Sun) will occur 1.30-1.48 Myr from now at a distance of 0.10 to 0.44 pc. The earlier and pioneering study of Garcia-Sanchez et al. (2001) (which motivated my work) also found GL 710 to be the closest approaching star, based on the original Hipparcos reduction and radial velocities available at the time. They found
perihelion to occur at 1.36 ± 0.04 Myr at a distance of 0.34 ± 0.18 pc. Note that these are 1sigma error bars, which are 68% confidence intervals. In my paper I quote 90% confidence intervals. For the reasons I give in section 1 of the paper, I believe my confidence interval to be a more realistic estimate of the uncertainties. But these are still subject to some assumptions.
Mamajek et
al. posted a paper on arXiv on 16 Feb. 2015 claiming that W0720 is
the closest encounter. Can you comment on this?
This is a nice study. They have taken the existing data on a recently-discovered low mass star (W0720) and performed orbital integrations to determine the distribution of encounter times and distances according to the observational uncertainties. I've used the simple linear motion approximation (i.e. assuming the star moves on a constant velocity relative to the Sun up to the encounter - see section 3.2 of my paper) to confirm that their results are roughly right (I get d=0.25 pc and t=-71kyr), and the confidence limits look okay. As the star is currently so close by, the gravitational potential they use is unimportant. So assuming their input data are correct, their encounter is valid (unless W0720 happened to pass very close to some other star since its encounter, but that is highly unlikely.) Having found the parameters of the close encounters, they do a back-of-the-envelope calculation of the effect it may have had on the Oort cloud. Answer: very small, as you'd expect for such a low mass star travelling at high speed.
They say this is the closest known stellar encounter to the Sun. My study uncovered an apparently closer encounter ( Hip 85605), but as I pointed out in my paper and as Mamajek et al. correctly discuss, the data on this star are of poor quality, so it's not a robust result. However, the second closest encounter I find, GL 710 (Hip 89825), comes almost as close to the Sun as W0720 - the mean approach distance is just 0.02 pc larger. (Several previous authors have also found that GL 710 will come very close to the Sun.) This is well within the uncertainties in the closest approach distance of either star, so I don't think one need dwell on which is "closer".
Nor is this particularly important. There are so many low mass and very faint M, L, and T dwarfs out there which we haven't discovered yet, that I am quite sure we will find many more which come even closer to the Sun than W0720 or GL710. The Mamajek et al. study is the latest step in this process.
But finding "the" closest star is not really the big question (although it would be very interesting if we found a star that came/will come really close to the Sun, say within a few hundred AU!). Like W0720 and GL710, most of these low mass close encounters will have a negligible effect on the Oort cloud compared to the Galactic tide or other more massive stellar perturbers. And that's the point: more distant encounters of more massive and/or slower-moving stars can have a much larger effect. W0720 has a mass of just 0.15 Msol and at 83 km/s is moving more than twice as fast as typical encounters. A star the mass of the Sun moving at the typical encounter speed (34 km/s) would have a similar gravitational influence on the Sun at a distance of 1pc as W0720 does at its perihelion. And we know many stars like this. (Here I have assumed that the size of the perturbation goes as M/(d^2*v), where M is the mass of the star, d the closest approach distance, v the speed at closest approach. If one instead uses M/(d*v) as a proxy for the size of the perturbation, then the Sun-like star has the same effect as far out as 4pc.)
So if one is interested in the history of the perturbation of the Oort
cloud, we cannot focus on just the closest encounters. We need to
look at the population of encounters out to larger distances (a few
pc). Studies (such as mine) have already found more massive and/or
slower encounters which are expected to have a much larger impact on
the Oort cloud than either W0720, GL710, or the other very close
encounters we have found. An example is Gamma Microscopii (Hip
103738), a G6 giant with a mass of about 2.5 Msol, which had an
expected closest approach of 0.83 pc 3.8 Myr ago. This would have
seven times the perturbing effect of W0720 (using M/(d^2*v)).
Section 4.3 of my paper lists some other massive candidates.
Which stars are likely to approach within 0.5pc and how long do they take to cross the Oort cloud?
I find five stars to come within 0.5pc (the first five lines of Table 3). However, as I note in section 4.2, some of these have poor data. So if you want more reliable identifications, the five closest approaches are Hip nos. 89825 (GL 710), 85661, 103738 (gamma Mic), 71683 (alpha Cen A) and 71681 (alpha Cen B). There are notes on all of these in section 4.2 of the paper. The Alpha Cen system is essentially at perihelion now.
The Oort cloud crossing time can be calculated from an assumed size of the Oort cloud and the star's perihelion speed (which can be taken to be constant during the crossing to a good approximation). As I mention in section 5.5, even if one took the Oort cloud to be as large as 1pc in diameter, the crossing time for a perihelion speed of 34 km/s (the median for close encounters in my sample) is only 30 kyr. This is shorter than all the other uncertainties involved (and discussed in section 5).
van Maanen's star is currently 14 light years away. Could it really have encountered the Sun just 15 000 years ago?
Yes! The Hipparcos parallax puts van Maanen's star, the closest
solitary white dwarf to the Sun, at a distance of 4.3 pc, which is
indeed about 14 light years. It's radial velocity is 263 km/s
relative to the Sun. Translating a speed of 1 km/s into pc and years,
we find that 1 km/s is equivalent to 1 pc in 1 million years, to within a few
percent. Since its encounter, the relative speed and direction of van
Maanen's star hasn't changed that much, so we can calculate the
approximate distance it has travelled in 15,000 years using the simple
formula distance = speed x time, which gives us 4 pc. Note that van
Maanen has a relatively high relative speed compared to many other
stars in the study. Some of the stars appear to have even higher
relative speeds, but some of these may be errors in the input
catalogues. Note however, that we do know of stars with such high
speeds relative to the Galactic centre that they will escape from the
Galaxy.
Will the stars you identify actually disrupt the Oort cloud?
One could make a more detailed study of the individual encounters, and in fact this is precisely what a PhD student of mine and I plan to do in the next months. One needs to adopt a model for the Oort cloud, the details of which are only weakly constrained by current data. But given this and details of the incoming star, one can run models and make predictions. There exist several papers which do precisely this for some assumed incoming star. Without wanting to preempt the outcome of our study, I think we can safely predict that comet orbits would indeed be disrupted by the closest encounters. What remains to be seen is by how much, and what the flux of comets in the inner solar system would be, and thus what the probability is (as a function of time) of the Earth being hit. (That probability is never zero, by the way. The issue is by how much it varies, and how high can it get.)
I've heard that the Galactic tide also affects the Oort cloud. Did you take that into account?
I do not model the perturbation of the Oort cloud in this paper. I just trace orbits. This uses an (admittedly simple) model for the Galactic potential (i.e. mass distribution), so this includes the effect of the tide. A gravitational tide is essentially a gradient in the gravitational force due to all the stars and dark matter in the Galaxy. The dominant component of the Galactic tide acting on the solar system is the one perpendicular to the Galactic disk. The Sun probably oscillates quasi-periodically (not a strict period) about the Galactic disk with a period of around 50-80 Myr (it's not well constrained by current data; see for example section 6 of my 2009 review paper) so the tide is likewise quasi-periodic.
If you want to know more about the long-term solar orbit and the possible effect of stellar encounters and the tide on the Oort cloud, see the recent paper by me and my PhD student.
How will data from Gaia help improve this study, in particular the connection to impact craters on the Earth?
Gaia can help in a number of ways. First, it will better determine the local Galactic environment: It will measure with higher accuracy the current positions and velocities of the stars I have used in my study, but it will also detect many more and measure their properties (position, velocity, mass) much better. That is, we get a better sample with which to make a connection to the impact craters. This is not only because we see more of the stars, but also because we can better account for what we don't see. Second, it will better measure the gravitational potential of the Galaxy, including spiral arms and giant molecular clouds, thus permitting a better tracing of the stellar orbits. Third, it will better determine the positions and velocity of Sun star relative to this Galaxy potential, permitting us to better trace the Sun's orbit (which is also necessary, because the Sun too moves relative to the Galaxy).
But it will still always be hard to connect the times of stellar encounters to the dates of impact craters, for the reasons I give in section 5.5 of the paper. Ultimately there are few impact craters which have been caused by comets (200 in total, most are due to asteroids), and there is a large and uncertain time lag between an encounter and any possible impact.
Is there observational evidence for the Oort cloud or is it just a theoretical concept?
The Oort cloud was first conjectured to exist by Ernst Öpik in 1932 and the idea developed further by Jan Oort in 1950, in order to explain the existence and orbital properties of the long period comets. The basic idea is that such comets should not be observable if there is not a large reservoir in the outer solar system to replenish them. There are no direct observations of objects in the Oort cloud - they are far too faint for current telescopes. The size and properties of the Oort cloud are therefore inferred based on the comets we can observe and theoretical considerations about the origin of the solar system. Estimates vary, but it's expected to contain 1012 to 1013 bodies larger than 1km diameter. That's a lot, but the total mass is only of order a few Earth masses.
By asking "or is it just a theoretical concept?" you suggest that only direct observations (=fuzzy images?) of a few Oort cloud members would turn it into "fact". Yet theoretical considerations (here Newtonian dynamics and the evolution of the solar system) and "indirect" observations (here of the long-period comets and the observed properties of the solar system) tell us enough about the Oort cloud to claim a very high probability that it exists. This is often the way things are done in science. "Direct" observation is often not possible or does not provide better evidence for the existence of something. A lot of interpretation and analysis goes into converting an image of an exoplanet, say, into evidence for an exoplanet. Yet precisely in that field we have far better evidence from "indirect" observations of exoplanets. One might choose to get lost in semantic issues here: Is a transit light curve a direct or indirect observation? The distinction is not sharp and is anyway unimportant. What counts is the strength of evidence it provides. (One may suggest "direct" means "model independent". But I would argue that any observation must be interpreted and therefore involves a model at some level.)
In analogy with the Oort cloud, has the core of the Earth ever been "seen"? Have we ever observed the nuclear fusion in the Sun? No, but I would say they have been "observed" in a broader (and more useful) sense of the word, as we have a lot of data which enable us to constrain with confidence what is going on. I wouldn't say that the Oort cloud is on such a firm basis as these, and I wouldn't deny that image, spectra or velocity measurements of Oort cloud objects would not be useful. But I do want to make the point that science has very successfully used "indirect" observations to allow us to learn and to gain confidence in an explanation. The Oort cloud is such a case.
Could future humans use close encounters as a shortcut to visit an exoplanets?
It seems that many if not most stars host exoplanets. What you are suggesting is not really a technological or temporal short cut, however. Travelling to a star passing our solar system at a distance of around 1 pc with a relative speed of 30 km/s is no easier than travelling the the nearby stars (the nearest of which is just over 1 pc away). And we would have to wait 10s of thousands of years for the next encounter. If we can ever achieve interstellar travel, I don't suppose it would take that long to achieve, so why wait?
Do these close encountering stars present a threat to the Earth? Should we worry?
A close encountering star is likely to perturb the Oort cloud sufficiently to increase the flux of comets entering the inner solar system. Let's not forget, however, that this kind of perturbation is happening all the time due to the gravitational effect of the Galaxy as whole, and due to stars which encountered even earlier. That is, there is a "background" of comets entering the inner solar system which we cannot necessarily associate with a particular stellar encounter. This is also because the time between an encounter and the time that comets enter the inner solar system could be many or even many tens of millions of years, much longer that than the typical time between close encounters.
While a close encounter would indeed increase the chance per year of the Earth being hit by a comet, the increase in asbsolute risk is very small: it increases from a very, very small value to just a very small value. It's also not a rapid increase: we're talking over hundreds of thousands, or millions of years. Of course, given a long enough time scale then it's inevitable that something large will be on a collision course with the Earth (but more likely a Near-Earth Asteroid), just as it's highly likely that a supervolcano will go off within the next few million years. These are real, but very long term risks, and not worth worrying about now given that humanity faces equally significant risks on much shorter timescales from human-generated catastrophes (international aggression, environmental destruction, antibiotic resistance, etc.)
Just for the record: I think we should be monitoring the sky to
identify objects which may hit the Earth. During a human lifetime
we're far more likely to be hit by something relatively small which
causes local rather than global damage. Such small objects and short
timescales are unrelated to my study.
Some websites are saying you have predicted the apocalypse. Comments?
Yawn.